Key management – Secgroup Ca' Foscari

We now discuss how keys are managed, stored and checked by parties and KDC servers.

Symmetric key management

We have seen that practical authentication protocols based on symmetric keys require the presence of a centralised trusted party that shares one long-term key with each possible user. It is important to have a way to securely deal with these keys so that an attack to the KDC system would not necessarily compromise the keys of all users.

An interesting solution to this problem is provided by symmetric key certificates. The trusted party possesses a master key $K_M$ that it only knows. When a new user $U$ is registered, the respective long-term key $k_U$ is generated and is encrypted under the master key together with the identifier and additional information such as the key lifetime, type, etc. For example $SCert_U = E_{K_M}(U,k_U,L)$ certifies that user $U$ has key $k_U$ with lifetime $L$ .

These certificates can be distributed to users together with their keys and users can freely distribute their certificates to other users, since the encryption under the master key protects the confidentiality of the enclosed keys. The trusted party can completely forget about the keys and ask for certificates when needed. As an example, let us consider again the Kerberos protocol. The first message $A,B,N_A$ representing a request from A to B with nonce $N_A$ , would be replaced by $SCert_A,SCert_B,N_A$ . The KDC decrypts the two certificates and obtains the keys for Alice and Bob together with their identifiers, that will be enclosed in next messages for Alice: $E_{K_A}(k_s,B,N_A,{L}),E_{K_B}(k_s,A,{L})$ . After these messages have been generated, $K_A,K_B$ can be deleted.

Asymmetric key management

The idea of certificates is even more important for protocols based on asymmetric keys. In this case, in fact, it is crucial that key management is completely decentralised since we do not want any on-line centralised servers available at each protocol execution.

First notice that the relevant property here is authenticity of public keys. If Alice and Bob want to communicate they need a way to check that public key is the one truly associated with the opposite party. Suppose Alice wants to send Bob a secret message M. It is insecure for Bob to simply send his public key to Alice:

$\begin{array}{l} B \rightarrow A: PK_B \\ A\rightarrow B: E_{PK_B}(M) \end{array}$

In fact, an attacker can replace $PK_B$ with his own key:

$\begin{array}{cccl} E(B) & \rightarrow & A &: PK_E \\ A & \rightarrow & E(B) & : E_{PK_E}(M) \end{array}$

The attacker can then decrypt the secret message encrypted under his public key.

We need a mechanism that allows Alice to check that the received key is the one belonging to Bob. Public key certificates contains the same informations as the symmetric key ones but, instead of being encrypted under a symmetric master key, they are signed by a Certification Authority (CA), a trusted entity that certifies the authenticity of user’s public keys. For example $Cert_B = B, PK_B, L, sign_{CA}(B, PK_B, L)$ . If Alice knows the public key of the CA and Bob sends this certificate, then Alice can check the validity of the key and its association with Bob (B). The protocol becomes:

$\begin{array}{l} B \rightarrow A: Cert_B \\ A\rightarrow B: E_{PK_B}(M) \end{array}$

The attacker cannot change the public key as he is not able to forge a signature from the CA.

Generating real certificates with openssl

We now show all the steps required to generate a ‘root’ CA certificate, i.e., the self-signed certificate holding the CA public key that Alice and Bob use to verify their respective public keys. OpenSSL allows for executing all of these operation via command-line. The root CA key and certificate can be generated as follows:

$ openssl req -x509 -newkey rsa:2048 -keyout cakey.pem -out cacert.pem
Generating a 2048 bit RSA private key
......+++
.......................................................................
.....................................+++
writing new private key to 'cakey.pem'
Enter PEM pass phrase:
Verifying - Enter PEM pass phrase:
-----
You are about to be asked to enter information that will be incorporated
into your certificate request.
What you are about to enter is what is called a Distinguished Name or a DN.
There are quite a few fields but you can leave some blank
For some fields there will be a default value,
If you enter '.', the field will be left blank.
-----
Country Name (2 letter code) [AU]:IT
State or Province Name (full name) [Some-State]:Italy
Locality Name (eg, city) []:Venice
Organization Name (eg, company) [Internet Widgits Pty Ltd]:Ca' Foscari
Organizational Unit Name (eg, section) []:DAIS
Common Name (eg, YOUR name) []:DAIS CA
Email Address []:CA@dais.unive.it
$ ls
cacert.pem	cakey.pem
$

We now have a self signed certificate cacert.pem (option -x509) and a new private key cakey.pem, protected via a pass phrase. If we want to use these as if they were from a CA, we need to save them in a directory structure as follows (index.txt and serial are needed for tracking certificate generation):

$ mkdir demoCA
$ mkdir demoCA/private
$ mkdir ./demoCA/newcerts
$ mv cacert.pem demoCA/
$ mv cakey.pem demoCA/private/
$ touch demoCA/index.txt
$ echo 10 > demoCA/serial

Alice and Bob can now send to the CA their certificate signing requests (CSRs) that the CA signs, producing two certificates that are given to the two users. CSRs are generated by Alice and Bob as follows:

$ openssl req -newkey rsa:1024 -keyout Alice_key.pem -out Alice_req.pem
Generating a 1024 bit RSA private key
.....................++++++
...............................++++++
writing new private key to 'Alice_key.pem'
Enter PEM pass phrase:
Verifying - Enter PEM pass phrase:
-----
You are about to be asked to enter information that will be incorporated
into your certificate request.
What you are about to enter is what is called a Distinguished Name or a DN.
There are quite a few fields but you can leave some blank
For some fields there will be a default value,
If you enter '.', the field will be left blank.
-----
Country Name (2 letter code) [AU]:IT
State or Province Name (full name) [Some-State]:Italy
Locality Name (eg, city) []:Venice
Organization Name (eg, company) [Internet Widgits Pty Ltd]:Ca' Foscari
Organizational Unit Name (eg, section) []:DAIS
Common Name (eg, YOUR name) []:Alice
Email Address []:alice@dais.unive.it

Please enter the following 'extra' attributes
to be sent with your certificate request
A challenge password []:
An optional company name []:
$ ls
Alice_key.pem	Alice_req.pem	demoCA
$

We now have a new key, let’s say for Alice, in Alice_key.pem and a CSR in Alice_req.pem. The CSR is what we send to the CA to be signed, producing the final certificate for Alice public key. In particular the CSR contains Alice public key but NOT the private key, so that it can be safely sent in the clear. Suppose the CA has received the CSR. It can now produce the certificate as follows:

$ openssl ca -in Alice_req.pem -out Alice_crt.pem
Using configuration from /opt/local/etc/openssl/openssl.cnf
Enter pass phrase for ./demoCA/private/cakey.pem:
Check that the request matches the signature
Signature ok
Certificate Details:
        Serial Number: 16 (0x10)
        Validity
            Not Before: Dec 27 15:38:00 2011 GMT
            Not After : Dec 26 15:38:00 2012 GMT
        Subject:
            countryName               = IT
            stateOrProvinceName       = Italy
            organizationName          = Ca' Foscari
            organizationalUnitName    = DAIS
            commonName                = Alice
            emailAddress              = alice@dais.unive.it
        X509v3 extensions:
            X509v3 Basic Constraints: 
                CA:FALSE
            Netscape Comment: 
                OpenSSL Generated Certificate
            X509v3 Subject Key Identifier: 
                FE:21:20:5B:E4:D3:AF:71:A0:DC:7A:A8:1C:1C:26:14:82:C8:30:DD
            X509v3 Authority Key Identifier: 
                keyid:95:B5:F5:4A:57:55:C9:F3:38:0C:8A:23:71:0D:C7:3E:47:7B:EF:FD

Certificate is to be certified until Dec 26 15:38:00 2012 GMT (365 days)
Sign the certificate? [y/n]:y

1 out of 1 certificate requests certified, commit? [y/n]y
Write out database with 1 new entries
Data Base Updated
$

We have produced the certificate for Alice in file Alice_crt.pem, signed by the CA. Suppose now that Bob wants to communicate with Alice and he possesses the CA root certificate cacert.pem. He can check Alice certificate as follows:

$ openssl verify -CAfile demoCA/cacert.pem Alice_crt.pem 
Alice_crt.pem: OK
$

This confirms that Alice certificate is correctly signed by the CA represented by cacert.pem. The public key can be extracted from the certificate as follows:

$ openssl x509 -pubkey -in Alice_crt.pem 
-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQC0QW9fGLEsTG8F2m3HBDxlNhkS
UBersW1y3cl878+MACzYHa6kwtaKZF7VQyEKrvVwXVMUzwAq2+0gD+Xr1WGehrpU
66epyhpr2j9lbQ9Xz3w1GlCAli3PkN9TGlH2lX/V+10O2T1XT94DOKOttGL0NKVQ
PIaXaqiMVVDfTr3FvwIDAQAB
-----END PUBLIC KEY-----
$

And of course Bob can query about the subject and email:

$ openssl x509 -subject -email -in Alice_crt.pem 
subject= /C=IT/ST=Italy/O=Ca' Foscari/OU=DAIS/CN=Alice/emailAddress=alice@dais.unive.it
alice@dais.unive.it
$

Now Bob can use this public key knowing that it belongs to Alice, as far as he trusts the DAIS CA identified by the cacert.pem certificate.

The Transport Layer Security (SSL/TLS) protocol. When we connect to a web site using https, the SSL/TLS protocol establishes a secure, encrypted session. The association of the identity and the public key of the web server is checked using certificates and the asymmetric key of the web server is used to establish a new session key. Any subsequent communication is encrypted under the session key. To allow for certificate check, browsers include a number of built in CA root certificates. For a web site it is enough to require a web site certificate from one of these official CA’s.

Sometimes, we connect to sites that have generated their own certificates. In these cases the browsers warn that something is wrong and that the certificate cannot be checked. Accepting the certificate is at our own risk: it could be the case that there is a man-in-the-middle attacker setting up a fake site using a self signed certificate, and intercepting/modifying all subsequent messages (sniffing our credentials, modifying the bank transfers we perform, etc.). If we store permanently the certificate, next connections will be guaranteed to be with the same server as the previous one, but this does not prevent we are under a man-in-the-middle attack right now, of course.

Certificate chains

Having just root CA’s signing any certificate in the world does not scale well. It is useful in practice to have different levels of certifications (maybe associated with countries, states, cities, etc.) so that the end user can go the ‘local’ CA. To deal with this hierarchical organisation of CA’s we need to be able to check certificate chains: The root CA certifies the next CA in the hierarchy and so on all the way to the end user. Once we provide the whole chain, it is enough to trust the root public key in order to check all the certificates in the path to the end user.

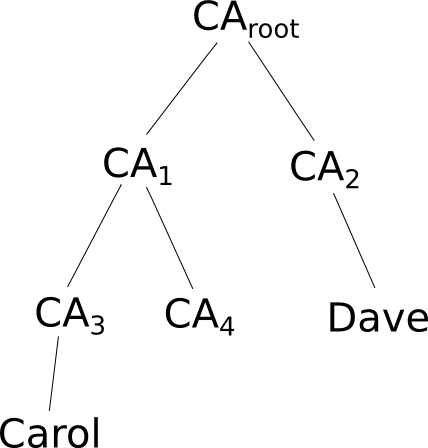
Above we illustrate two end users Carol and Dave certified by two different CAs under the same root CA. If Carol wants to communicate with Dave, she needs to send Dave the certificate chain from the root CA to herself: $\mathrm{CA}_1$ certificate signed by $\mathrm{CA}_{root}$ , $\mathrm{CA}_3$ certificate signed by $\mathrm{CA}_1$ and Carol’s certificate signed by $\mathrm{CA}_3$ .

To give a practical example with openssl, we can think of Alice as an intermediate CA certifying Bob. Above, we have already generated a certificate for Alice signed by our DAIS CA. In a similar way we can generate a certificate for Bob signed by Alice. Since Alice certificate is signed by the DAIS CA, if Eric wants to check Bob’s certificate he would need the whole path from the CA to Bob which is CA->Alice->Bob.

This is Bob’s certificate signed by Alice (we leave as an exercise the generation of Bob’s certificate, notice that openssl uses default paths to look for CA certificates and keys. These paths can be changed in the configuration file):

$ cat Bob_crt.pem 
Certificate:
    Data:
        Version: 3 (0x2)
        Serial Number: 32 (0x20)
        Signature Algorithm: sha1WithRSAEncryption
        Issuer: C=IT, ST=Italy, O=Ca' Foscari, OU=DAIS, CN=Alice/emailAddress=alice@dais.unive.it
        Validity
            Not Before: Dec 28 10:38:38 2011 GMT
            Not After : Dec 27 10:38:38 2012 GMT
        Subject: C=IT, ST=Italy, O=Ca' Foscari, OU=DAIS, CN=Bob/emailAddress=bob@dais.unive.it
        Subject Public Key Info:
            Public Key Algorithm: rsaEncryption
                Public-Key: (1024 bit)
                Modulus:
                    00:c2:29:58:40:7d:7f:e5:5e:e3:f2:d4:52:b0:3f:
                    37:e0:4e:07:66:23:ce:80:57:71:08:85:b5:4b:73:
                    75:ff:89:7d:a3:5d:73:5a:98:13:cf:54:90:ff:56:
                    d7:fc:39:0a:ff:c6:91:dd:aa:21:53:c0:11:6e:da:
                    b2:a2:cd:67:9a:f9:17:16:f4:dc:56:bf:94:42:11:
                    a3:11:aa:2e:44:7a:b6:3e:ca:d3:46:60:d4:a7:0d:
                    7c:fe:98:37:09:3e:02:28:5e:23:a2:86:cf:e4:85:
                    2c:e2:eb:31:ac:ff:a2:3a:63:34:ad:0c:dc:a5:99:
                    24:0c:0f:73:58:65:a4:0e:f7
                Exponent: 65537 (0x10001)
        X509v3 extensions:
            X509v3 Basic Constraints: 
                CA:FALSE
            Netscape Comment: 
                OpenSSL Generated Certificate
            X509v3 Subject Key Identifier: 
                F7:13:39:AE:9B:4D:67:02:F1:8A:32:15:9D:B3:D4:AF:EF:57:B5:E9
            X509v3 Authority Key Identifier: 
                keyid:FE:21:20:5B:E4:D3:AF:71:A0:DC:7A:A8:1C:1C:26:14:82:C8:30:DD

    Signature Algorithm: sha1WithRSAEncryption
        52:16:69:db:62:43:f2:15:66:7d:61:c4:a1:37:0d:c7:86:41:
        c8:31:4e:9c:bf:0f:9f:63:3c:b8:dc:61:fb:1e:5c:88:f1:a0:
        e2:62:47:25:5f:48:48:a7:67:72:20:3a:e1:b0:06:18:89:b5:
        9f:f8:62:90:d2:16:2d:42:79:af:96:21:df:c6:ac:93:69:a0:
        53:11:ef:18:16:f3:b9:96:b2:e5:79:5c:c0:76:40:ce:bb:84:
        ad:14:43:c0:96:a8:88:e1:57:e6:0e:1a:56:3f:45:d2:a2:32:
        dc:f6:18:3c:3a:a6:8b:c5:e2:68:0e:2b:dc:4b:2d:8c:c5:da:
        bd:55
-----BEGIN CERTIFICATE-----
MIIC2TCCAkKgAwIBAgIBIDANBgkqhkiG9w0BAQUFADB2MQswCQYDVQQGEwJJVDEO
MAwGA1UECAwFSXRhbHkxFDASBgNVBAoMC0NhJyBGb3NjYXJpMQ0wCwYDVQQLDARE
QUlTMQ4wDAYDVQQDDAVBbGljZTEiMCAGCSqGSIb3DQEJARYTYWxpY2VAZGFpcy51
bml2ZS5pdDAeFw0xMTEyMjgxMDM4MzhaFw0xMjEyMjcxMDM4MzhaMHIxCzAJBgNV
BAYTAklUMQ4wDAYDVQQIDAVJdGFseTEUMBIGA1UECgwLQ2EnIEZvc2NhcmkxDTAL
BgNVBAsMBERBSVMxDDAKBgNVBAMMA0JvYjEgMB4GCSqGSIb3DQEJARYRYm9iQGRh
aXMudW5pdmUuaXQwgZ8wDQYJKoZIhvcNAQEBBQADgY0AMIGJAoGBAMIpWEB9f+Ve
4/LUUrA/N+BOB2YjzoBXcQiFtUtzdf+JfaNdc1qYE89UkP9W1/w5Cv/Gkd2qIVPA
EW7asqLNZ5r5Fxb03Fa/lEIRoxGqLkR6tj7K00Zg1KcNfP6YNwk+AiheI6KGz+SF
LOLrMaz/ojpjNK0M3KWZJAwPc1hlpA73AgMBAAGjezB5MAkGA1UdEwQCMAAwLAYJ
YIZIAYb4QgENBB8WHU9wZW5TU0wgR2VuZXJhdGVkIENlcnRpZmljYXRlMB0GA1Ud
DgQWBBT3Ezmum01nAvGKMhWds9Sv71e16TAfBgNVHSMEGDAWgBT+ISBb5NOvcaDc
eqgcHCYUgsgw3TANBgkqhkiG9w0BAQUFAAOBgQBSFmnbYkPyFWZ9YcShNw3HhkHI
MU6cvw+fYzy43GH7HlyI8aDiYkclX0hIp2dyIDrhsAYYibWf+GKQ0hYtQnmvliHf
xqyTaaBTEe8YFvO5lrLleVzAdkDOu4StFEPAlqiI4VfmDhpWP0XSojLc9hg8OqaL
xeJoDivcSy2Mxdq9VQ==
-----END CERTIFICATE-----
$

We can check the chain as follows:

$ cat Alice_crt.pem Bob_crt.pem > chain.pem
$ openssl verify -CAfile demoCA/cacert.pem chain.pem
chain.pem: OK
$

If we omit Alice certificate verification fails, as expected:

$ openssl verify -CAfile demoCA/cacert.pem Bob_crt.pem 
Bob_crt.pem: C = IT, ST = Italy, O = Ca' Foscari, OU = DAIS, CN = Bob, emailAddress = bob@dais.unive.it
error 20 at 0 depth lookup:unable to get local issuer certificate
$

Chains can be arbitrarily long.

Further extensions

The basic hierarchal tree organisation illustrated above can be extended to multi-trees, where many root CAs are present (as typically happens in browsers): if any users know many root CAs it is enough a chain from one of the roots to a leaf to certify the corresponding user. To avoid storing all the root certificates, root CAs might certify each other so that any root CA is ‘reachable’ by any other.

Interestingly, there are solutions where no centralised authorities are required. In Pretty Good Privacy (PGP) it is proposed a web-of-trust: any user can trust other users. The level of trust might be such that if Alice trusts Bob, any other user certified by Bob is trusted by Alice. In a sense, each user can ‘elect’ other users as CA’s that can be trusted when signing certificates for other users. This can be depicted as a general graph with no roots: a path in the graph represents a chain of certificates from oner user to the other. If we trust the starting user, we can successfully verify the identity and public key of the final user in the path.