RSA is the most famous asymmetric-key cipher. It is based on a few technical results from number theory that we recall below.
Background
The Euler function. The Euler function returns the number of numbers less than or equal to
that are coprime to
. Recall that
and
are coprime iff
, i.e., if the only common divisor is 1. So, for example, we have that
since 1 and 2 are coprime to 3,
since only 1 and 3 are coprime to 4 and so on. We report some values below:
We prove this result for with
primes. The numbers less than
that are not coprime to
is exactly the multiples of
and
, i.e.,
that are
. Now we have that
.
The Euler Theorem. Let and
be coprime, i.e.,
. Then
.
Proof. Let be the
numbers less than
and coprime with
. We consider
and we show that
. We need a few lemmas:
Lemma 1. Let be coprime to
. Then
is coprime to
.
Proof. This can be easily proved by considering that all divisors of are products of divisors of
or
. Thus a common divisor of
and
must also divide
and/or
. Thus,
would imply that
or
giving a contradiction.
Lemma 2. Let be coprime to
. Then
is coprime to
.
Proof. Since we have that any common divisor
of
and
must divide
. In fact,
that implies
is an integer value.
Lemma 3. Let with
. Then
.
Proof. We have . Thus
that implies
and so
. Since
we have that
must divide
and so
, i.e.,
.
Now, by Lemma 1 and 2 we have that all numbers in set are coprime to
and smaller than
. Since
is the set of all numbers coprime to
and smaller than
we obtain that
. Now, consider
and
in
. Since
is coprime to
, by Lemma 3 we obtain that
implies
, which give a contradiction. Thus we have that
for all
and
. This proves that
.
To conclude the proof it is enough to observe that . Since all
are coprime to
, by applying many times Lemma 3 we obtain
, which is what we wanted to prove.
The RSA cipher
RSA stands for Rivest-Shamir-Adleman, the authors of the cipher in 1978. We let with
big prime numbers. We also let
and
be such that
. The public key is
while the private key (secret trapdoor) is
. We let
. Encryption is defined as
while decryption is
.
We now show the correctness of the cipher, i.e., that decrypting under the private key a plaintext encrypted under the public key gives
. Notice that
implies
for some
. What we need to prove is that
. In fact, if this holds we have
. In this case we know that Euler theorem holds, and we directly have that
which implies
, giving the thesis;
. In this case, since
we have that either
or
. Without loss of generality we assume
(the proof for the other case is identical). We now have
for some
and
. Euler theorem gives
, which implies
. This implies
giving
for some
. We obtain
.
Implementation
As we will discuss, RSA requires a big modulus of at least 1024 bits. With these sizes, implementation becomes an issue. For example a linear complexity
, that is typically considered very good, is prohibitive as it would require at
steps. Every operation should in fact be polynomial with respect to the bit-size
.
Basic operations
We first observe that basic operations such as sum, multiplication and division can be performed in , respectively, by using simple standard algorithms (the one we use when we compute operations by hand). Reduction modulo
amounts to compute a division which is, again,
.
Exponentiation
This operation is used both for encryption and decryption. First notice that we cannot implement exponentiation to the power of as
multiplications. In fact, public and private exponents can be the same size as
. Performing
multiplications would then require
operation, i.e.,
which is like brute-forcing the secret trapdoor and infeasible for
. We thus need to find some smarter, more efficient way to compute this operation.
There exists a much faster algorithm, known as Square-and-Multiply, that is based on the following observation: when we rise a number x to a power of 2 such as 8, instead of performing 7 multiplications we can simply compute which is just 3 multiplications. In general, if the exponent is not a power of 2, we can exploit a similar trick by performing some additional multiplications when needed. For example
can be done as
: after squaring twice we multiply the result by
so that we have
. With a final square we obtain the result.
In particular can be written as
which is
and finally
. Intuitively, if the exponent is even we divide it by 2 and we square, if it is odd we get one
out (which is an additional multiplication) and we proceed as above. Dividing the exponent by 2 amounts to follow its binary representation. For example, 10 is 1010.
We start from the most significant bit. At each step we square and, only when we have a 1 we multiply by . A python implementation follows:
def squareAndMultiply(x,e):
r=1
b = bin(e)[2:] # binary representation of e, removes the 0b
for bit in b: # for all bits of exponent
r = (r*r) # we always square
if bit=='1':
r = (r*x) # we multiply only if bit is 1
return r
The number of steps in the worst case is for the two multiplications, iterated
times, giving
. Thus for 1024 bits we can expect about 1 billion steps, which is still efficient on modern machines.
A few examples follow:
>>> squareAndMultiply(2,8)
256
>>> squareAndMultiply(2,10)
1024
>>> squareAndMultiply(2,20)
1048576
>>> squareAndMultiply(2,1024)
17976931348623159077293051907890247336179769789423065727343008115773267580550096313270847732240753
60211201138798713933576587897688144166224928474306394741243777678934248654852763022196012460941194
53082952085005768838150682342462881473913110540827237163350510684586298239947245938479716304835356
329624224137216L
>>> squareAndMultiply(2,2048)
32317006071311007300714876688669951960444102669715484032130345427524655138867890893197201411522913
46368871796092189801949411955915049092109508815238644828312063087736730099609175019775038965210679
60576383840675682767922186426197561618380943384761704705816458520363050428875758915410658086075523
99123930385521914333389668342420684974786564569494856176035326322058077805659331026192708460314150
25859286417711672594360371846185735759835115230164590440369761323328723122712568471082020972515710
17269313234696785425806566979350459972683529986382155251663894373355436021354332296046453184786049
52148193555853611059596230656L
>>>
Inverse modulo 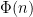
This operation is necessary to compute the private exponent from the public one. Recall that RSA requires . To find these two numbers, one technique is to choose
and to compute its multiplicative inverse modulo
. This is guaranteed to exist, by the Euler theorem, when
. In this particular case, there is also an efficient algorithm to compute the inverse based on the Euclidean algorithm for computing
.
We recall the Euclidean algorithm, written in iterative style:
def Euclid(c,d):
while d != 0:
tmp = c % d
c = d
d = tmp
return c
The idea is that, to compute , when
, we can compute
since it can be easily seen that they are the same. This algorithm terminates in
, given that the number of iterations is
. This latter fact can be proved by observing that every 2 steps we at least halve the value d. Assume that after one step this is not true, i.e.,
. Next step will compute
giving the thesis. We know that halving leads to a logarithmic complexity, i.e., linear with respect to the number of bits
.
We now extend the algorithm so to compute the inverse modulo whenever
. We substitute the computation of
with
q = c//d # integer division
tmp = c - q*d # this is c % d
We add two extra variables e and f and we save the initial value of d in d0, as follows:
def EuclidExt(c,d):
d0 = d
e = 1
f = 0
while d != 0:
q = c//d # integer division
tmp = c - q*d # this is c % d
c = d
d = tmp
tmp = e - q*f # new computation for the inverse
e = f
f = tmp
if c == 1:
return e % d0 # if gcd is 1 we have that e is the inverse
For example
>>> EuclidExt(5,17)
7
>>> 7*5 % 17
1
>>> EuclidExt(14,17)
11
>>> 14*11 % 17
1
>>>
To see the correctness of the algorithm, we need two auxiliary variables g and h, initialized with 0 and 1, and updated as e and f, i.e.,
tmp = g - q*h # new computation for the inverse
g = h
h = tmp
Let c0 and d0 note the initial values of c and d, at each iteration it holds e * c0 + g * d0 = c and f * c0 + h * d0 = d. This can be proved by induction:
- Base case: at the beginning we have c0 = c, d0 = d, e = 1, f = 0 and g = 0, h = 1. Thus e * c0 + g * d0 = c0 = c and f * c0 + h * d0 = d0 = d.
- Inductive case: we assume e * c0 + g * d0 = c and f * c0 + h * d0 = d hold and we prove they hold after c, d, e, f, g and h are updated. Since c, e and g are updated with the values of d, f and h, respectively, we have that e * c0 + g * d0 = c holds because of f * c0 + h * d0 = d. Variables d, f and h are updated as c – q*d, e – q*f and g – q*h. Thus, f * c0 + h * d0 = (e – q*f) * c0 + (g – q*h) * d0 = e * c0 + g * d0 – q*( f*c0 + h * d0) = c – q*d = d, which gives the thesis.
Thus, when we return e % d0 we have that c is 1 and the invariant e * c0 + g * d0 = c = 1 implies that ( e * c0 + g * d0 ) % d0 = 1, i.e., (e * c0) mod d0 = 1, which by definition means that e mod d0 is the inverse of c0 modulo d0.
Generating RSA exponents
We can thus pick a random public exponent and compute its inverse modulo
. This works if we are lucky and
is coprime to
. This happens quite frequently. It can be proved that two random numbers are coprime with probability ~0.6. Thus iterating this 2-3 times should give a suitable pair of public, private exponents.
In practice, however, it is often the case that the public exponent is a fixed constant, typically the prime number . Using a low exponent improves the performance of encryption (recall that each 1 in the exponent requires an extra multiplication). In this case, of course, we have to choose
so that
is not a multiple of 65537.
RSA and factorization: Notice that knowing makes it very simple to compute the private exponent. Factoring
into
allows for computing
. Thus we now understand that RSA security is based on the infeasibility of factoring the modulus
. For this reason we require
to be at least 1024 bits. Numbers of this size are still considered impossible to factor in a reasonable time. A size of 2048 is however already suggested for critical applications. Moreover, if we compute
we can easily factor
since we have a system of 2 equations with two variables
:
Primality test
We finally see how to generate two big prime numbers. The oldest algorithm for finding prime numbers is due to Eratosthenes and is known as the “Sieve of Eratosthenes”. In order to discover all prime numbers less than or equal N we write all numbers from 2 to N. We then start from the smallest (2, initially) that we call p and we remove from the list all of its multiples 2p, 3p, … We iterate the procedure by picking the smallest p survived from previous steps.
At the end, the remaining numbers are guaranteed to be prime since they are not multiples of any smaller number. The algorithm can be optimized by removing multiples starting from . In fact, any smaller
with
would have been removed at a previous step when checking the multiples of
. This also implies that we can stop when p is the square root of N. A simple python implementation follows:
import sys, math
def Sieve(N):
Ns = int(math.sqrt(N)) # square root of N
sieve = set(range(2,N+1)) # sets are good to model the 'sieve'
for p in range(2,Ns+1):
if p in sieve: # for all survived numbers
for q in range(p*p,N+1,p): # we remove multiples bigger that p*p
sieve.discard(q)
print sieve # sieve have only primes
For example
>>> Sieve(22)
set([2, 3, 5, 7, 11, 13, 17, 19])
>>>
Unfortunately this algorithm takes at least steps meaning
for the smallest RSA modulus.
Instead of generating all the primes we pick them at random and test their primality. There are many probabilistic efficient algorithms for primality test. In 2002, Agrawal, Kayal and Saxena proposed the first deterministic algorithm for primality test in the paper “PRIMES is in P” published on Annals of Mathematics. This is a very important result but the proposed algorithm is much slower with respect to existing probabilistic ones, as it costs which makes it rather slow for
.
Miller-Rabin test: Here we illustrate one of the most famous probabilistic primality tests due to Miller and Rabin. The algorithm is a NO-biased Montecarlo, meaning that it is always correct for the NO answer (the number is not prime) but can be wrong for the YES case (the number is prime). The probability of being wrong, however, is less than a constant . This allows for iterating the test until the error is small enough: by running the test r times, the probability that it says YES and the number is not prime is less than
, i.e., it decreases exponentially with respect to the number of iterations. For example if we pick
we have an error with probability less than
which is less than brute-forcing a typical symmetric key, and so small to be negligible.
Let us now illustrate the algorithm:
Prime(n):
write n-1 = 2^k * m
pick a random a such that 1 < a < n
b = a^m mod n
if b == 1:
return True
for i in range(0,k):
if b == n-1:
return True
b = b*b mod n
return False
Theorem. the above algorithm is always correct on False answers (NO-biased).
Proof. Assume, by contradiction, that the algorithm returns False but the number n is prime. False is only returned at the last step which means the algorithm ‘survived’ all the if branches. In particular we have that . Moreover
, for
. By the assumption that n is prime and by Euler theorem we know that
. In summary we have:
It is now sufficient to notice that each of the above values is the square of the preceding one. Since the last one () is equal to 1 we have the the previous (
) is a square root of 1 modulo n, i.e., it is 1 or n-1. Now we know that it is different from n-1 which implies it is 1. We iterate (backward) this on all the values until we get
which gives a contradiction. This proves that the algorithm can never return False if n is prime.
A working python implementation follows. Notice the use of squareAndMultiply for exponentiation (this is necessary if we want to test large primes)
def Prime(n):
m = n-1
k = 0
while (m&1 == 0): # while m is even
m = m>>1
k += 1
a = random.randrange(2,n)
b = squareAndMultiply(a,m,n)
if b == 1:
return True
for i in range(k):
if b == n-1:
return True
b = b*b % n
return False
For example:
>>> from primality import *
>>> Prime(3)
True
>>> Prime(5)
True
>>> Prime(8)
False
>>> Prime(11522209602914035334582776765168233041221730674213419598532382197901576899621082
564579279226654163047918553777391630395657069138498001131991904807951650901)
True
>>>
Generating RSA primes
How can we finally generate big primes? We simply generate them at random and we test their primality. This takes about steps, where n is the upper bound of the interval we choose from. It can be proved, in fact, that about 1 out of
numbers less than n are prime. For example, if we want 512 bits of size (for a modulus of 1024) we have that
. Thus, on average, after 358 attempt we should find a prime number of size 512 bits.
Notice that the Miller-Rabin algorithm should be iterated to lower as needed the probability of error in case of successful answer. Even if the original paper proved that such a probability is bounded by , in a subsequent paper [1] it has been shown that the algorithm is much more precise that that. In practice this is the suggested number of iterations from NIST (Appendix C.3): 7,4 and 3 for 512, 1024 and 1536 bits, with an error probability of
, meaning that the test requires very few iterations to give a prime with high probability.
Case study
openSSL uses a number of iterations slightly bigger than the one suggested above. For a 1024 key we have:
$ openssl genrsa 1024
Generating RSA private key, 1024 bit long modulus
.............................++++++
..........++++++
e is 65537 (0x10001)
-----BEGIN RSA PRIVATE KEY-----
MIICWwIBAAKBgQCgEsd7T2jArgJsusd2bXXR0D5JjUnvccwiDuEJXtk6AhZcOHSX
kWxPWvgskXMDXxgNZtyYr3aC8VYEP83yVj6qH/T5fueWH0O0reygy1LTLfvbp56F
g/52ssCwQCLtFjIEPu93Sa5MR5d2iJ9LKamE22qGbiSmQvfOJLMAtarkcQIDAQAB
AoGAEbpCsVtYBI7A4f3FfU4eEEB5xXeKSqRVsSfosDr637u/cjMmZmrKjfdLKNRq
4mKzrThJEffMri/AEPRoAICgq9XJn3AlW1CC9F7ISs2K/BUKYkvHHHQsqQsyR+Y+
EISmtVtYGUW0ShKfqtO61DmDbrtWlCn4BZRFUfyTzIPyTckCQQDOR7DLWBlRl6tI
ldTTUnytnxHvbsQuZIMBMdDhYRDOjBPjHAT2h0gMRbstp4fqJguT8+7jKeHZ29yE
LZDlbf9DAkEAxqfzNi2FxFnSvANJ5MAoOXNQhWqme5WtJ+Hc4ffelSGrt/lgfAMe
OtWqlmCFOpZw7YuhnHe27TRFpa2tnjGwOwJAXi8HfuC7trBcaWjX4qDgAloF01+s
vU3xLsNzDuTFyrjUf7aUYYeFEu1nuEGs4fD7ClOvOBMwZstnFQbFCKw/hwJAD0MZ
+WCX9VTdTtqF09A7huZoGkfuUHJYYkcE/EtZy2VR1wmOsxheOzDtMS5rLewe8vEW
UnoUELdCXo8wVoYEvwJAWhpesKH6cA7+sYZk2PK6edEPHnRCP6eewnG5M14CTin9
DR0N0kkoOdybAY/V8CbhqTMlrE3g7+pchbAe83OmuA==
-----END RSA PRIVATE KEY-----
The six occurrences of ‘+’ represent six iterations of the Miller-Rabin test.
References
[1] I. Damgard, P. Landrock, and C. Pomerance, C. “Average Case Error Estimates for the Strong Probable Prime Test” Mathematics of Computation, v. 61, No, 203, pp. 177-194, 1993.
